Hey, it's been a while, hasn't it? It's my fault. I've been busy doing several things, but in compensation I have an unfinished SQL Injection post, which I calculate that it will be finished in a few weeks
Well, this post is a bit off-topic, but I wanted to bring you, something different from the usual. As last year I behaved very well, the Three Wise Men, have given me a ProxMark3. So I took an old bus card that I had... and here it is were all started.
The first thing I did was to run hf search to check if it was a high frequency card.
proxmark3> hf search
UID : 17 fd 45 0c
ATQA : 00 04
SAK : 08 [2]
TYPE : NXP MIFARE CLASSIC 1k | Plus 2k SL1
proprietary non iso14443-4 card found, RATS not supported
No chinese magic backdoor command detected
Prng detection: WEAK
Valid ISO14443A Tag Found - Quiting Search
proxmark3>
The next thing I did, was to try some default keys.
proxmark3> hf mf chk *1 ?
--chk keys. sectors:16, block no: 0, key type:?, eml:n, dmp=n checktimeout=471 us
No key specified, trying default keys
chk default key[ 0] ffffffffffff
chk default key[ 1] 000000000000
snip...
chk default key[16] 533cb6c723f6
chk default key[17] 8fd0a4f256e9
To cancel this operation press the button on the proxmark...
--.
No valid keys found.
proxmark3>
But, no luck. The following I did, was to look for a dictionary with more keys, and I found this one. But again, no luck. As I was starting on this topic of RFID cards. I looked up some information and concluded that the key is made up of 12 characters in hexadecimal... And yeeeeah, I did what some of you may have thought. I wrote a small Python script, which created all possible combinations of 12 characters in hexadecimal.
Before we start getting into the matter, I want you to know that all the possible combinations would be 16^12 (281,474,976,710,656).
I will divide the post in several parts, in which each part, I will explain a problem that appeared, and a solution. So, lets jump in :)
Part 1
The key here, was to get a dictionary in hexadecimal, which was composed of all possible combinations formed by 12 characters. After unsuccessfully looking up dictionaries in Google, GitHub... I decided to do it on my own, with the following script which I took from here.
I edited the script, replacing the :010X, by :012X (this would generate 12 characteres instead of 10), ran the script and redirected the output to a file called dictionary.txt. Finally I splited the terminal and launched watch -n1 ls -lh to see the size of the file.
Amazingly, with only one minute of execution, the file size was 1.3 GB!!!

So obviously I couldn't leave it running because I would run out of space. Therefore, I thought about dividing the combinations by sections to go discarding.
Part 2
My idea here, was to create dictionaries by number of characters, and within those dictionaries, make sub-dictionaries so that they do not become so heavy.
First of all, we need to find out what number we need to raise 16, in order to create patterns. Let me explain. First, I created a dictionary (5.txt) that was formed only by the first 5 characters, and the other values were at zero, this means 0000000AAAAA. Where A, is any hexadecimal value.
In this case is not to hard, we just need to calculate 16^5 and we get that we would have a total of 1048576 possible combinations. Let's edit the script so it looks like this:
def gen_all_hex():
i = 0
while i < 16**5:
yield "{:012X}".format(i)
i += 1
for s in gen_all_hex():
print(s)That generated a file of 1048576 lines, so it is useful to verify that everything has gone well. The size of the file, in case someone asks, was 13 Mb.
The next thing I did was to run a brute force with the ProxMark, and the dictionary we just created. Buuut... A very interesting thing happened that I will investigate soon. Something happened, that made me think that there might be a Buffer Overflow in the ProxMark3 application... let's see
When I executed the command and passed the dictionary we just created...
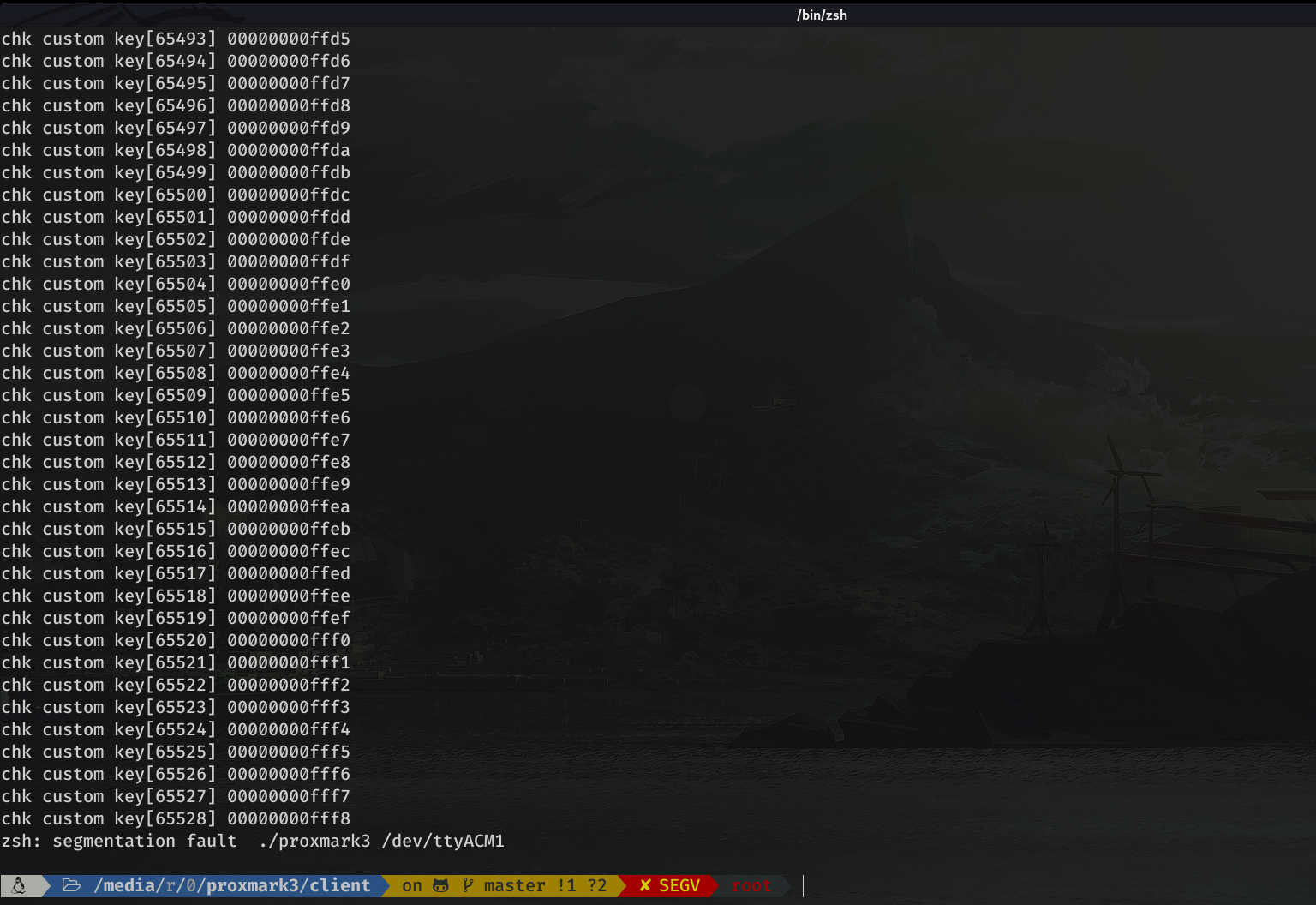
Mmmmm we get a segmentation fault... Check for a possible BOF, added to the to-do list.
Leaving this aside, it means that we cannot pass on so many keys. So, I tried to split the file in half to see if, with half of the keys, it did not cause a segmentation fault.
cat 5.txt | head -n$(python -c 'print(1048576 / 2)') > 5-1.txtBut then I realized that this was not necessary, since the program itself told us in which line the segmentation fault occurred. If we look at the last lines before the error. We see the next:
snip
chk custom key[65526] 00000000fff6
chk custom key[65527] 00000000fff7
chk custom key[65528] 00000000fff8
zsh: segmentation fault ./proxmark3 /dev/ttyACM1It seems that in the key nº 65528 the error has occurred. Since it is a key per line, we know that ProxMark only accepts dictionaries up to 65528 lines. The next thing I did was a test with a file of 65528 lines, and almost when it was 2 hours, I got a "Command execute timeout" error. Therefore I deduced that the list was still too big
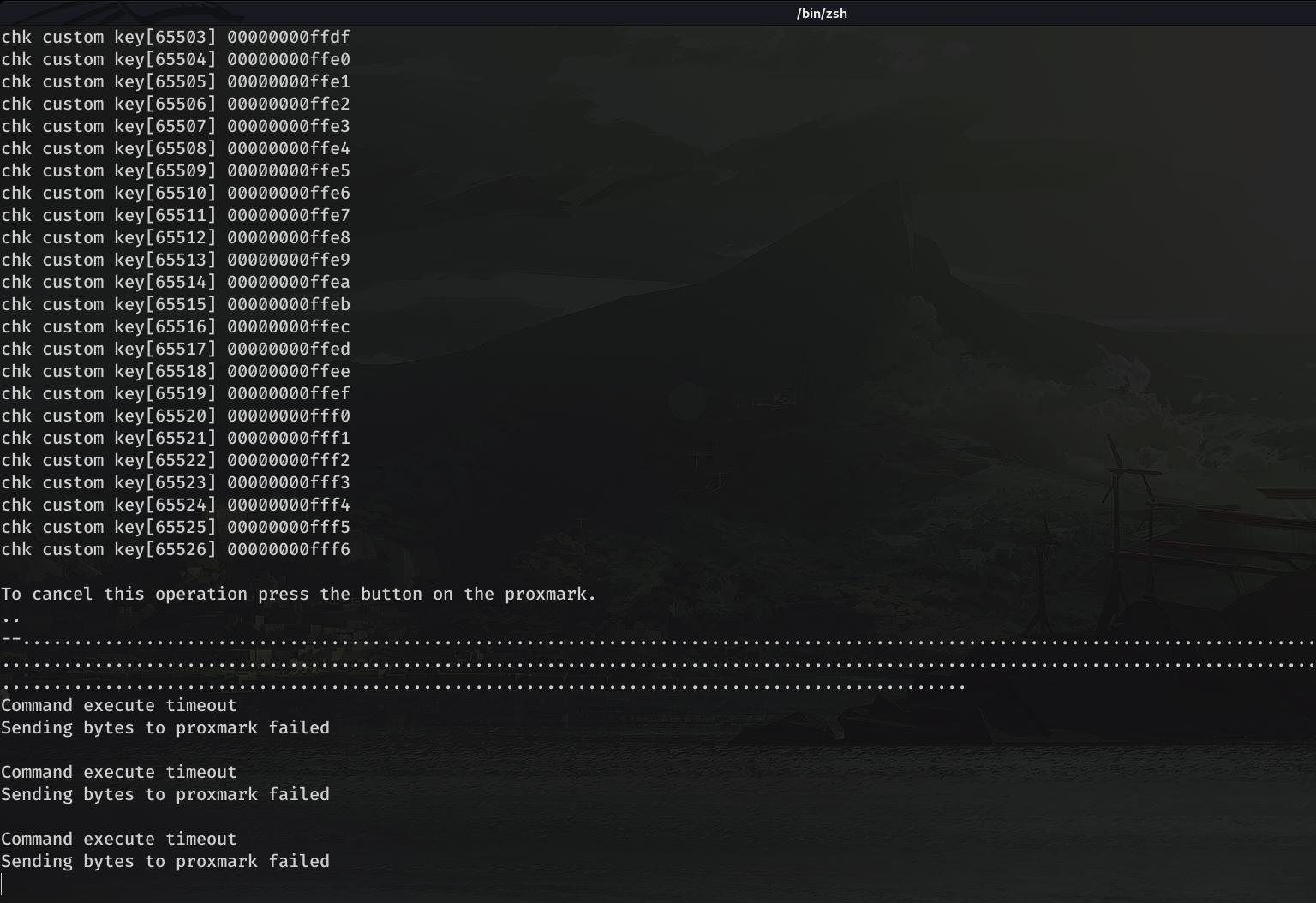
So, what I did, was to divide 65528 by 2, and pass a dictionary with 32764 lines, after 1 hour and 30 minutes, the program ended properly, and as expected, no key was valid.
Part 3
Now that I have to divide the 5.txt dictionary in sub-dictionaries, each sub-dictionary will be 5-n.txt where n will be the number corresponding to the sub-dictionary. We have to calculate, from which combination to which combination goes in a sub-dictionary without skipping any combination.
Taking into consideration that the number of lines in the 5.txt dictionary is 1048576 and that we can only make sub-dictionaries of 32764 lines. We will have to go adding 32764 to each, previous result, beginning from 0 to 1048576.
In this way, the first sub-dictionary would be in the range from 0 to 32764, the next one from 32764 to 32764*2, next from 32764*2 to 32764*3 and so on. I automated this with the next script:
#!/bin/bash
c="32764" #Counter
x="1" #First line
y="32764" #Last line
e="1048576" #Max lines
d="0" #Dictionary number
while [ $c -le $e ]; do
cat 5.txt | sed -n -e "$x,$y p" -e "$y q" > diccionario-$d.txt
let d=1+$d
let x=$x+32764
let y=$y+32764
let c=$c+32764
done
But at that moment, I realized, that starting from 0 all the combinations, was not a very good idea, because. How many keys have we seen of the type that are not AAAAAAAAAAAAAAAAAAAAAAA?
To give you an idea. Here, I show you in a dictionary of 1140 lines, that only 81 of them, begin by 0. That means (I'm talking based on this list) that only 7.1% of the keys start with 0.

Part 4
Because of this, I proposed to myself to edit the script a little bit in the way that it creates only combinations that fill all characters, i.e. AAAAAAAAAAAA. Because as we have seen, most of the passwords are AAAAAAAAAAAA. In this way I thought I could shorten the time of searching for the key, and at the same time increase the possibilities. But as we will see in the end... the numbers are still huge.
First of all, we must find out which number we have to put in the counter variable, which is i
Since we want the combinations to start from the hexadecimal number 100000000000 we have to convert that number into decimal, which corresponds to 17592186044416.
Another thing I wanted to do, is to save every 32764 combinations in a dictionary-n.txt where n=n+1. So I did the following script
fc = 0
c = 0
def gen_all_hex():
i = 17592186044416;
global c
while i < 16**12:
yield "{:012X}".format(i)
i += 1
c += 1
file = open("diccionario%s" % fc, "a")
for s in gen_all_hex():
s = s.lower()
if c == 32763:
file.write(s + "\n")
c = 0
fc += 1
file.close()
file = open("diccionario%s" % fc, "a")
else:
file.write(s + "\n")
It only took me 12 minutes to see that this was impossible. After 12 m there were 33580 dictionaries created and was still going through the combination 10004193f01f!!!!
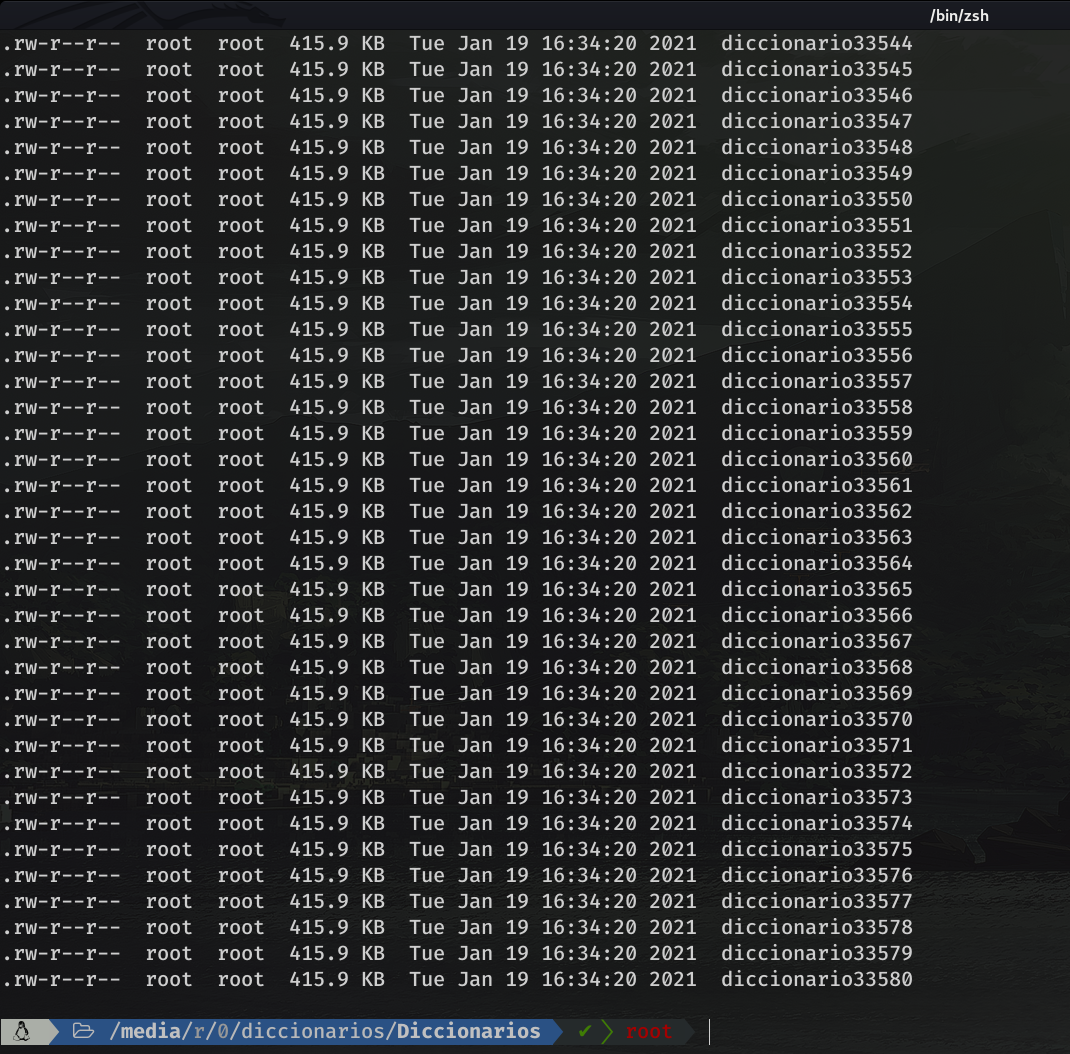
Bearing in mind that for every dictionary of 32764 combinations, it takes 1h 30 minutes more or less, to check those keys. And that in 12 m there were 33580 files. Doing the math ( considering that: 1 day = 1440 minutes and 1h 30m = 90m) it comes out a total of 16 dictionaries per day. So to check our 33580 dictionaries, we would need (33580 / 16) 2098 days. Just to check those combinations, since I stopped the script after 12 minutes. So, no longer imagine, check all the combinations (16^12 = 281,474,976,710,656).
I hope you liked this post, something out of the usual, but I wanted to make a post like this. Soon, as I learn and understand more about the subject, I will bring some post about RFID cards.
So, having said that, any doubt you may have, you can ask me through any of my social networks. I hope this post have served as food for your brains, see you in the next. Fire it up, baby.
